van Holde - Weischet Tutorial |
The Y-axis intercepts of the van Holde - Weischet extrapolation plot define the diffusion corrected S-values. For each division, a different fraction of the boundary is extrapolated to infinite time, and the sample sedimenting at that position in the boundary is shown with its respective S-value on the Y-axis. If the sample is homogeneous, all extrapolating lines will converge on a single point, the S-value of the (single component) sample. For multiple components, the divisions will extrapolate to multiple intercepts, indicating a range of S-values.
In order to map the S-value distribution, the boundary fractions for each division are plotted against their corresponding S-values. Vertical distributions then refer to homogeneous systems, distributions ranging over multiple S-values indicate sample heterogeneity.

Figure 6: Shown above is a full resolution van Holde - Weischet distribution plot of the 2-component experimental system shown on the previous page. For the construction of this plot, 14 scans have been analyzed with 100 equally spaced boundary fractions. The system clearly shows a 2-component system, with approximately 1.9 S for the slower sample (Chicken Lysozyme) and about 5 S for the faster component (208 bp dsDNA fragment).
Obtaining partial concentrations from distribution plots:
For non-interacting samples and samples displaying ideal,
concentration independent sedimentation behavior, the boundary fraction
number can be used to identify partial concentrations. In this example,
54% of the total boundary can be attributed to the faster component, while
approximately 37% of the boundary are accounted for by the slower component.
Depending on the quality of the data, small variations within the data
are normal and are caused by instrumental noise.
 |
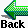 |
 |
This document is part of the UltraScan Software Documentation distribution.
Copyright 1998, 1999, The University of Texas Health Science Center at San Antonio.
The latest version of this document can always be found at:
Last modified on June 12, 1999.